Introduction to censCov

Sy Han (Steven) Chiou

2019-05-21

Source: vignettes/censCov-examples.Rmd

In this vignette, we demonstrate how to use the thlm function in censCov package to fit linear regression model with censored covariate using the methods proposed in Qian et al. (2018).

Notations

Suppose the linear regression model: \[ Y = \alpha_0 + \alpha_1X + \boldsymbol{\alpha}_2^\top \bf Z + \epsilon, \] where \(Y\) is the response variable, \(X\) is the covariate of interest which is subject to right censoring, \(\bf Z\) is a \(p\times 1\) vector of additional covariates that are completely observed, \(\epsilon\) is the random error term with mean 0 and finite variance, and the \(\alpha\)’s are the corresponding regression coefficients. We assume \(epsilon\) is independent of \(X\), \(\bf Z\), and \(C\), where \(C\) is the right censoring that potentially censors \(X\). The primary scientific interest is in the parameter \(\alpha_1\), which captures the association between \(Y\) and \(X\). The thlm function provides

  1. a test for \(H_o: \alpha_1 = 0\) against its complement;
  2. unbiased estimation of the regression coefficient of the censored covariate.

The thlm function

The thlm function presents the threshold regression approaches for linear regression models with a covariate that is subject to random censoring. The threshold regression methods allow for immediate testing of the significance of the effect of a censored covariate. The censCov package can be installed from CRAN with

> install.packages("censCov")

or from GitHub with

> devtools::install_github("stc04003/censCov")

The arguments of the thlm function are as follows:

> library(censCov)
> args(thlm)
function (formula, data, method = c("cc", "reverse", "deletion-threshold", 
    "complete-threshold", "all"), B = 0, subset, x.upplim = NULL, 
    t0 = NULL, control = thlm.control()) 
NULL
  • formula is a formula expression in the form of response ~ predictors. The response variable is assumed to be fully observed. The thlm function can accommodate at most one censored covariate, which is entered in the formula as an Surv object; see survival::Surv for more detail. If all the covariates are uncensored, the thlm function returns a lm object.
  • data is an optional data frame, list or environment contains variables in the formula and the subset argument. If this is left unspecified, the variables are taken from the environment from which thlm is called.
  • method is a character string specifying the threshold regression methods to be used. The following are permitted:
    • cc for complete-cases regression
    • reverse for complete-cases regression
    • deletion-threshold for complete-cases regression
    • complete-threshold for complete-cases regression
    • all for complete-cases regression
  • B is a numeric value specifies the bootstrap size for estimating the standard error of the regression coefficient for the censored covariate when method = "deletion-threshold" or method = "complete-threshold". When B = 0 (default), only the beta estimate will be displayed.
  • subset is an optional vector specifying a subset of observations to be used in the fitting process.
  • x.upplim is an optional number value specifies the upper support of the censored covariate. When left unspecified, the maximum of the censored covariate will be used.
  • t0 is an optional numeric value specifies the threshold when method = "deletion-threshold" or method = "complete-threshold". When left unspecified, an optimal threshold will be determined to optimize test power.
  • control is a list of threshold parameters including:
    • t0.interval controls the end points of the interval to be searched for the optimal threshold when t0 is left unspecified
    • t0.plot controls whether the objective function will be plotted. When t0.plot is true, both the raw t0.plot values and the smoothed estimates (using local polynomial regression fitting) are plotted.

Illustrative (simulated) data

We will illustrate the usage of thlm with a simulated data that is generated as below:

> simDat <- function(n) {
+   X <- rexp(n, 3)
+   Z <- runif(n, 1, 6)
+   Y <- 0.5 + 0.5 * X - 0.5 * Z + rnorm(n, 0, .75)
+   cstime <- rexp(n, .75)
+   delta <- (X <= cstime) * 1
+   X <- pmin(X, cstime)
+   data.frame(Y = Y, X = X, Z = Z, delta = delta)
+ }
> set.seed(1)
> head(dat <- simDat(200), 10)
            Y          X        Z delta
1  -1.4004305 0.25172728 5.432294     1
2  -0.6842887 0.39388093 3.359654     1
3  -0.5541144 0.04856891 1.545505     1
4   0.1832982 0.04659842 2.666390     1
5  -2.5467871 0.14535621 5.187083     1
6  -0.6450906 0.49887130 2.384249     0
7  -2.0134650 0.40985402 3.935176     1
8  -2.5030175 0.17989428 5.183661     1
9   0.6904316 0.31885583 1.355770     1
10 -1.4071626 0.04901533 4.513894     1

The columns in the simulated data set, dat, are

  • Y is the response variable
  • X is the covariate of interest when delta = 1 or the right censored value when delta = 0
  • Z is an additional covariate that is completely observed
  • delta is the censoring indicator for X

The average censoring percentage is about 20%.

Methods

The following methods for censored covariates are implemented in thlm.

Complete cases

When method = "cc", thlm removes rows with delta = 0 and fits the linear model via lm.

> thlm(Y ~ Surv(X, delta) + Z, data = dat, method = "cc")

 Call: thlm(formula = Y ~ Surv(X, delta) + Z, data = dat, method = "cc")

 Hypothesis test of association
H0: a1 = 0, p-value = 0.1028

or

> thlm(Y ~ X + Z, data = dat, subset = delta == 1)

 Call: thlm(formula = Y ~ X + Z, data = dat, subset = delta == 1)

 Hypothesis test of association
 H0: a1 = 0, p-value = 0.1047

The two \(p\)-values differs a bit because the thlm returns the Wald \(p\)-value.

Reverse survival regression

> summary(thlm(Y ~ Surv(X, delta) + Z, data = dat, method = "rev"))
Call:
thlm(formula = Y ~ Surv(X, delta) + Z, data = dat, method = "rev")

 Reverse survival regression

 Coefficients:
  Estimate   StdErr z.value p.value  
Y -0.18333  0.10056  -1.823  0.0683 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Deletion threshold regression

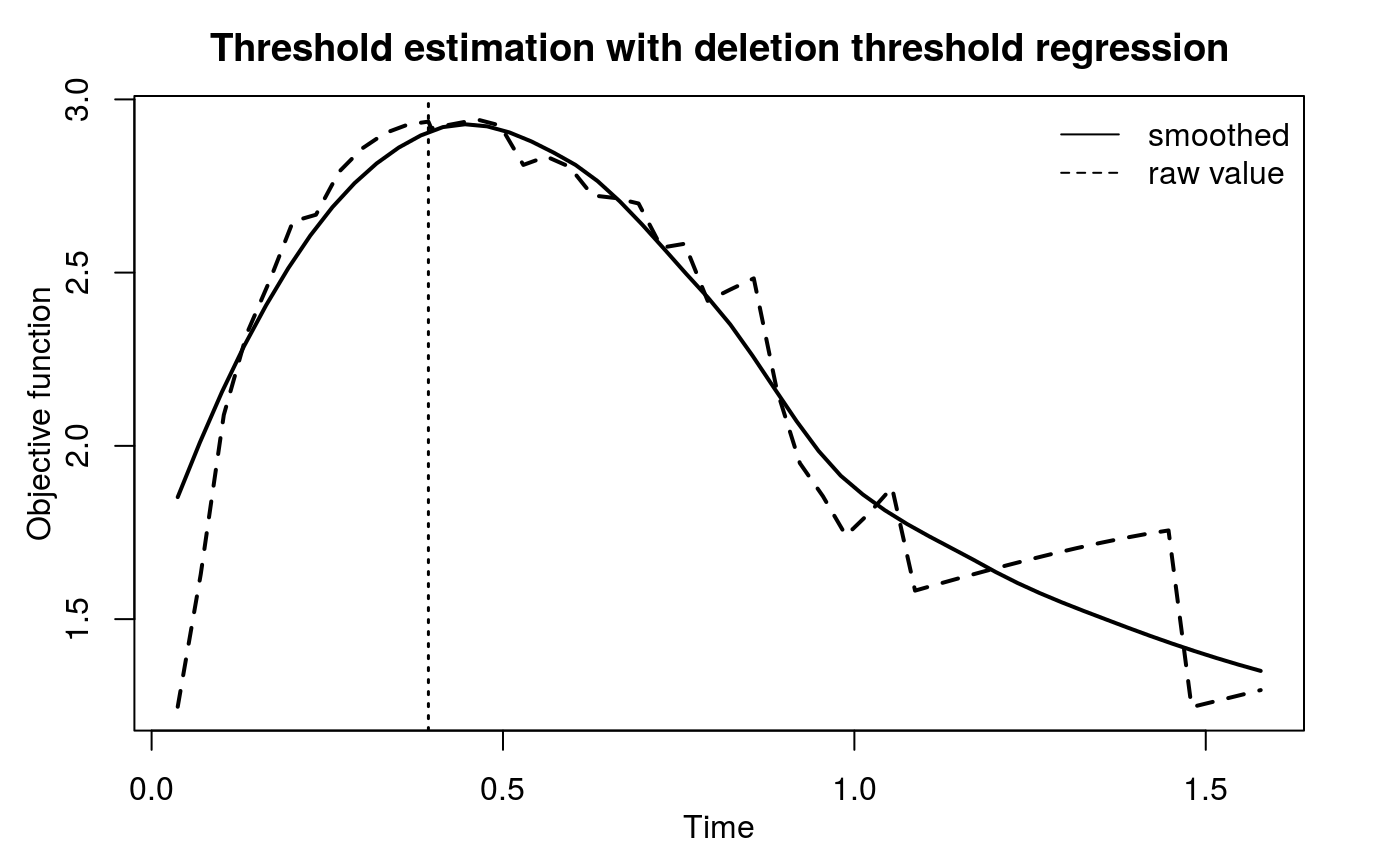
> summary(thlm(Y ~ Surv(X, delta) + Z, data = dat, method = "del", B = 100))

Call:
thlm(formula = Y ~ Surv(X, delta) + Z, data = dat, method = "del", 
    B = 100)

 Deletion threshold regression
 Optimal threshold is 0.394 

 Coefficients:
      Estimate    StdErr  z.value   p.value    
a1:X  0.642742  0.235796   2.7258  0.006414 ** 
a2:Z -0.527387  0.039061 -13.5018 < 2.2e-16 ***
b1:X  0.307045  0.117716   2.6084  0.009098 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Under the assumption that X is independent of Z given X*. See ?thlm for more detail.

Complete threshold regression

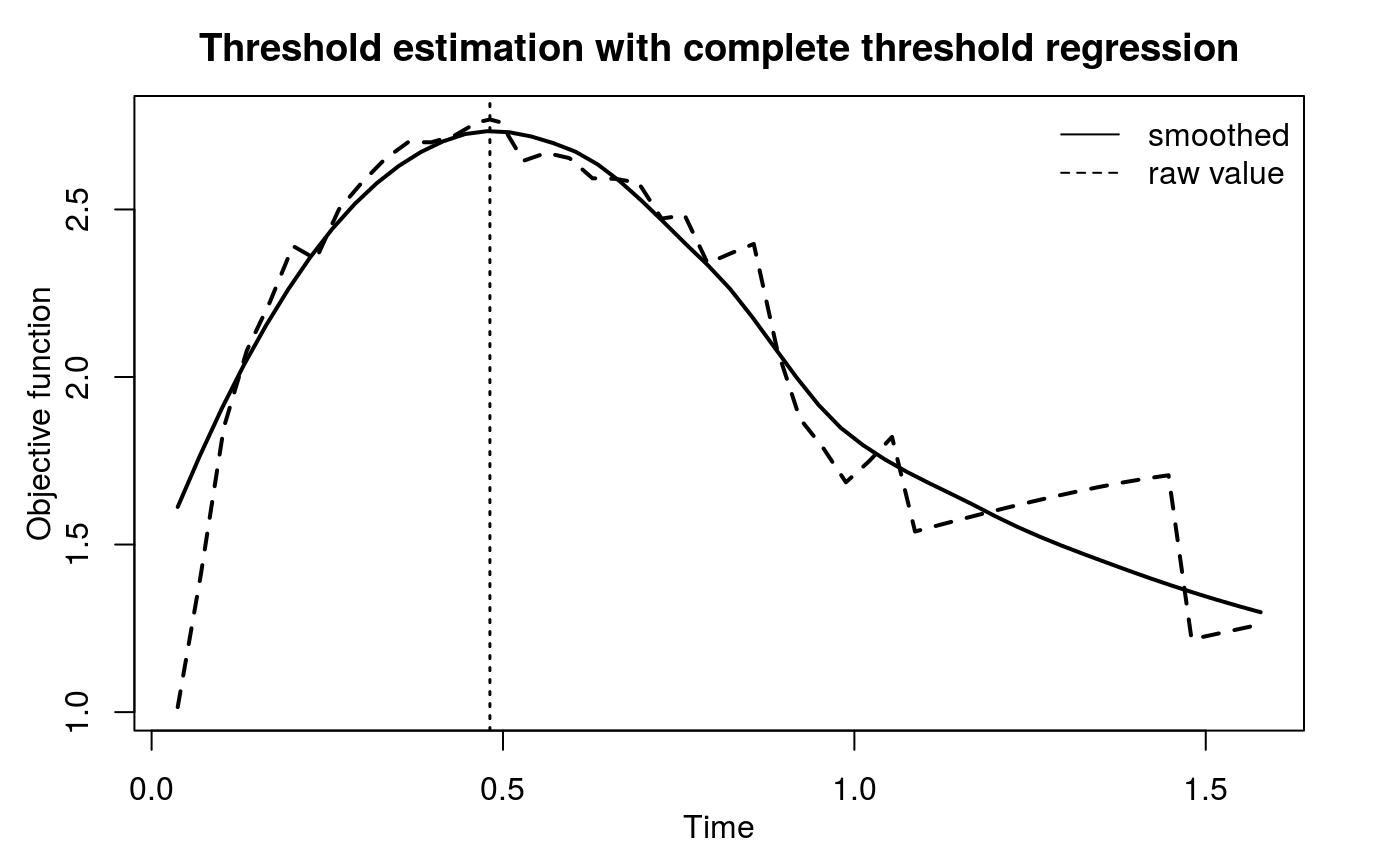
> summary(thlm(Y ~ Surv(X, delta) + Z, data = dat, method = "com", B = 100))

Call:
thlm(formula = Y ~ Surv(X, delta) + Z, data = dat, method = "com", 
    B = 100)

 Complete threshold regression
 Optimal threshold is 0.481 

 Coefficients:
      Estimate    StdErr  z.value p.value    
a1:X  0.368099  0.304016   1.2108  0.2260    
a2:Z -0.521533  0.036569 -14.2617  <2e-16 ***
b1:X  0.185574  0.138638   1.3386  0.1807    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Under the assumption that X is independent of Z given X*. See ?thlm for more detail.

All

The thlm function allows method = "all" that runs the complete cases analysis, reverse survival regression, deletion threshold regression, and complete threshold regression at once.

> summary(thlm(Y ~ Surv(X, delta) + Z, data = dat, method = "all", B = 100, 
+              control = list(t0.plot = FALSE)))
Call:
thlm(formula = Y ~ Surv(X, delta) + Z, data = dat, method = "all", 
    B = 100, control = list(t0.plot = FALSE))

Complete-case regression

 Coefficients:
   Estimate    StdErr  z.value p.value    
X  0.345912  0.212040   1.6314  0.1028    
Z -0.526268  0.040216 -13.0861  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Reverse survival regression

 Coefficients:
  Estimate   StdErr z.value p.value  
Y -0.18333  0.10056  -1.823  0.0683 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Deletion threshold regression
 Optimal threshold is 0.394
 Coefficients:
      Estimate    StdErr  z.value   p.value    
a1:X  0.642742  0.264088   2.4338  0.014941 *  
a2:Z -0.527387  0.039061 -13.5018 < 2.2e-16 ***
b1:X  0.307045  0.117716   2.6084  0.009098 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Complete threshold regression
 Optimal threshold is 0.481
 Coefficients:
      Estimate    StdErr  z.value p.value    
a1:X  0.368099  0.308850   1.1918  0.2333    
a2:Z -0.521533  0.036569 -14.2617  <2e-16 ***
b1:X  0.185574  0.138638   1.3386  0.1807    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Under the assumption that X is independent of Z given X*. See ?thlm for more detail.

FAQ

Can thlm fit model with one censored covariate (\(X\)) without any fully observed covaraite (\(Z\))?

Yes. For example:

> summary(thlm(Y ~ Surv(X, delta), data = dat, method = "all", B = 100, 
+              control = list(t0.plot = FALSE)))
Call:
thlm(formula = Y ~ Surv(X, delta), data = dat, method = "all", 
    B = 100, control = list(t0.plot = FALSE))

Complete-case regression

 Coefficients:
  Estimate  StdErr z.value p.value
X  0.10360 0.30109  0.3441  0.7308

Reverse survival regression

 Coefficients:
   Estimate    StdErr z.value p.value
Y -0.059851  0.076203 -0.7854  0.4322

Deletion threshold regression
 Optimal threshold is 0.394
 Coefficients:
     Estimate  StdErr z.value p.value
a1:X  0.49723 0.34765  1.4303  0.1526
b1:X  0.23753 0.16906  1.4051  0.1600

Complete threshold regression
 Optimal threshold is 0.481
 Coefficients:
     Estimate   StdErr z.value p.value
a1:X 0.082171 0.363501  0.2261  0.8212
b1:X 0.041426 0.196624  0.2107  0.8331

Under the assumption that X is independent of Z given X*. See ?thlm for more detail.

Can thlm fit model with one censored covariate (\(X\)) and multiple fully observed covaraites (\(Z\))?

Yes. For example:

> dat$Z2 <- dat$Z^2
> summary(thlm(Y ~ Surv(X, delta) + Z + Z2, data = dat, method = "all", B = 100, 
+              control = list(t0.plot = FALSE)))
Call:
thlm(formula = Y ~ Surv(X, delta) + Z + Z2, data = dat, method = "all", 
    B = 100, control = list(t0.plot = FALSE))

Complete-case regression

 Coefficients:
    Estimate    StdErr z.value  p.value   
X   0.350485  0.212926  1.6460 0.099754 . 
Z  -0.608191  0.216904 -2.8040 0.005048 **
Z2  0.011590  0.030151  0.3844 0.700687   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Reverse survival regression

 Coefficients:
  Estimate   StdErr z.value p.value  
Y -0.18087  0.10079 -1.7946 0.07272 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Deletion threshold regression
 Optimal threshold is 0.394
 Coefficients:
       Estimate    StdErr z.value  p.value   
a1:X   0.654823  0.253949  2.5786 0.009921 **
a2:Z  -0.623451  0.211023 -2.9544 0.003132 **
a3:Z2  0.013604  0.029366  0.4633 0.643169   
b1:X   0.312817  0.118646  2.6366 0.008375 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Complete threshold regression
 Optimal threshold is 0.481
 Coefficients:
        Estimate     StdErr z.value  p.value   
a1:X   0.3745097  0.2656319  1.4099 0.158575   
a2:Z  -0.5685414  0.1997397 -2.8464 0.004422 **
a3:Z2  0.0066448  0.0277542  0.2394 0.810784   
b1:X   0.1888058  0.1396247  1.3522 0.176299   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Under the assumption that X is independent of Z given X*. See ?thlm for more detail.

Does the censored covariate (\(X\)) need to be specified first in the formula?

Not nesscary. For exmaple:

> dat$Z2 <- dat$Z^2
> summary(thlm(Y ~ Z + Surv(X, delta) + Z2, data = dat, method = "all", B = 100, 
+              control = list(t0.plot = FALSE)))
Call:
thlm(formula = Y ~ Z + Surv(X, delta) + Z2, data = dat, method = "all", 
    B = 100, control = list(t0.plot = FALSE))

Complete-case regression

 Coefficients:
    Estimate    StdErr z.value  p.value   
X   0.350485  0.212926  1.6460 0.099754 . 
Z  -0.608191  0.216904 -2.8040 0.005048 **
Z2  0.011590  0.030151  0.3844 0.700687   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Reverse survival regression

 Coefficients:
  Estimate   StdErr z.value p.value  
Y -0.18087  0.10079 -1.7946 0.07272 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Deletion threshold regression
 Optimal threshold is 0.394
 Coefficients:
       Estimate    StdErr z.value  p.value   
a1:X   0.654823  0.274355  2.3868 0.016997 * 
a2:Z  -0.623451  0.211023 -2.9544 0.003132 **
a3:Z2  0.013604  0.029366  0.4633 0.643169   
b1:X   0.312817  0.118646  2.6366 0.008375 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Complete threshold regression
 Optimal threshold is 0.481
 Coefficients:
        Estimate     StdErr z.value  p.value   
a1:X   0.3745097  0.2989135  1.2529 0.210241   
a2:Z  -0.5685414  0.1997397 -2.8464 0.004422 **
a3:Z2  0.0066448  0.0277542  0.2394 0.810784   
b1:X   0.1888058  0.1396247  1.3522 0.176299   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Under the assumption that X is independent of Z given X*. See ?thlm for more detail.

Can thlm fit model with more than one censored covariate (\(X\))?

No.

Reference

Qian, Jing, Sy Han Chiou, Jacqueline E Maye, Folefac Atem, Keith A Johnson, and Rebecca A Betensky. 2018. “Threshold Regression to Accommodate a Censored Covariate.” Biometrics 74 (4). Wiley Online Library: 1261–70.